核心思想:点动成线,线动成面。
以下图为例,要求填充扇子的扇面部分。
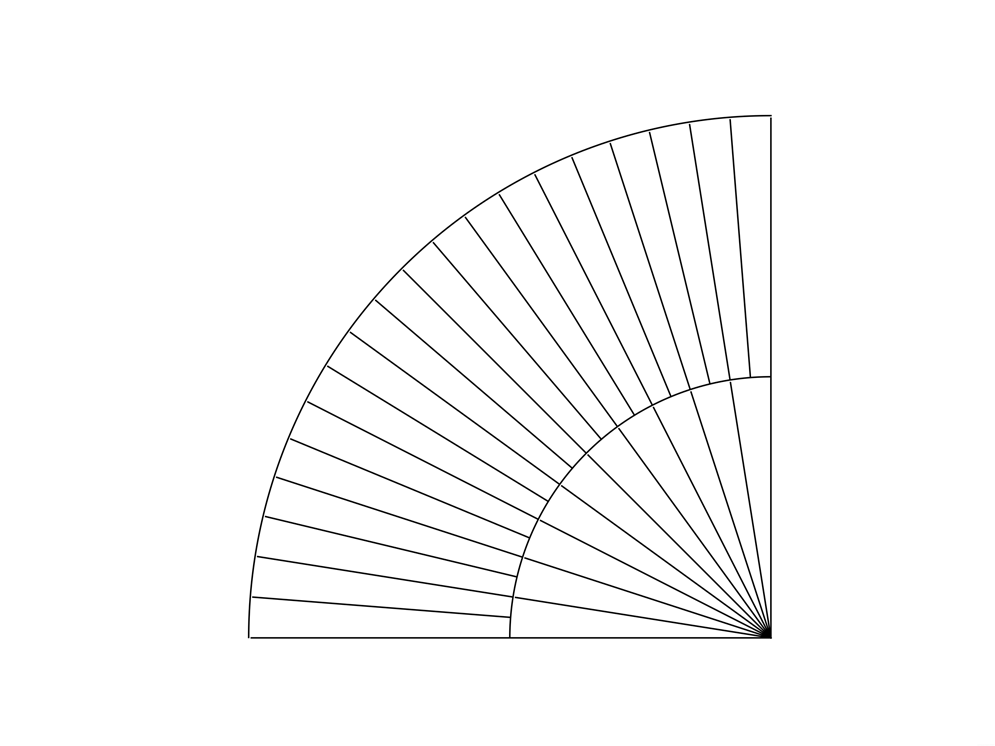
一、绘制扇子:
首先要弄清楚它的结构,即能够用代码把扇子绘制出来。(只有先把不规则图形的结构分析清楚,才能进一步填充它。)
先画一个框架:
#调用的库 import math import numpy as np import matplotlib.pyplot as plt
#画图的基础设置
fig = plt.figure(1)
ax = fig.add_subplot(111)
plt.axis('off')
plt.axis('equal')
#画框架线条 #画两条圆弧 theta = np.arange(0.5*np.pi,np.pi,0.01) for i in range(3): x = i * np.cos(theta) y = i * np.sin(theta) ax.plot(x,y,color='black',linewidth=0.7) #画两条主扇骨 z = np.arange(0,2,0.01) ax.plot(z * math.cos(math.pi/2), z * math.sin(math.pi/2), color='black',linewidth=0.7) ax.plot(z * math.cos(math.pi), z * math.sin(math.pi), color='black',linewidth=0.7)
如图:
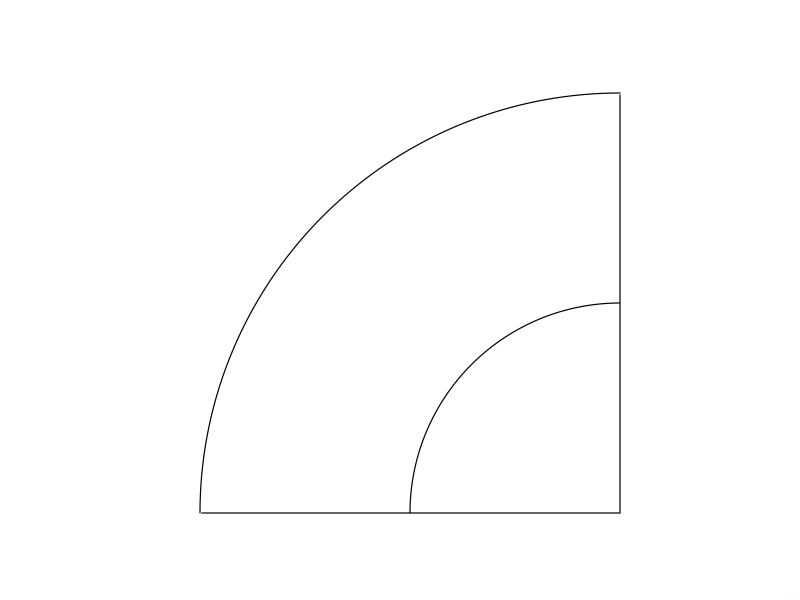
再把扇子细节部分画出来:
#画10根扇骨 z = np.arange(0,1,0.01) for i in range(11): ax.plot(z * math.cos(math.pi/2+i/10*math.pi/2), z * math.sin(math.pi/2+i/10*math.pi/2), color='black',linewidth=0.7) #扇面分割为20小份 z = np.arange(1,2,0.01) for i in range(0,21): ax.plot(z * math.cos(math.pi/2+i/20*math.pi/2), z * math.sin(math.pi/2+i/20*math.pi/2), color='black',linewidth=0.7)
这样就可以得到最开始的“素扇子”。
至此,我们也弄清了扇子的“数据”,扇面部分取1/4圆,扇骨部分通过np.arange()函数,把步长设置为0.01即可以创建一条半径,然后通过角度的正余弦变化构建扇骨,从而绘制出整个扇子。
二、填充扇子:
思路:如果两根扇骨的距离足够小,小到人眼难以分辨,当不同颜色的扇骨铺满扇面,就可以实现扇面的颜色填充。
#涂颜色
#选取一个涂色卡
color = ['#cde8f3','#91cfc9','#6bb3c0','#4198b9','#1e5670',
'#2d4e76','#99bcdd','#c4e5ef','#f3fafa','#bbabd0',
'#a16e8a','#643f5a','#cfbeb7','#f1ead7','#e99a9a',
'#e67b79','#f7cece','#eec9bc','#e1f1ea','#91c7c2']
#点动成线
z = np.arange(1.005, 2, 0.01)#边缘修正0.005,露出扇子轮廓
#线动成面
I = np.arange(0,20,0.01)
for i in I:
ax.plot(z * math.cos(math.pi/2+i/20*math.pi/2), z * math.sin(math.pi/2+i/20*math.pi/2), color=color[int(i)],linewidth=0.7,alpha=0.5)
如图所示:
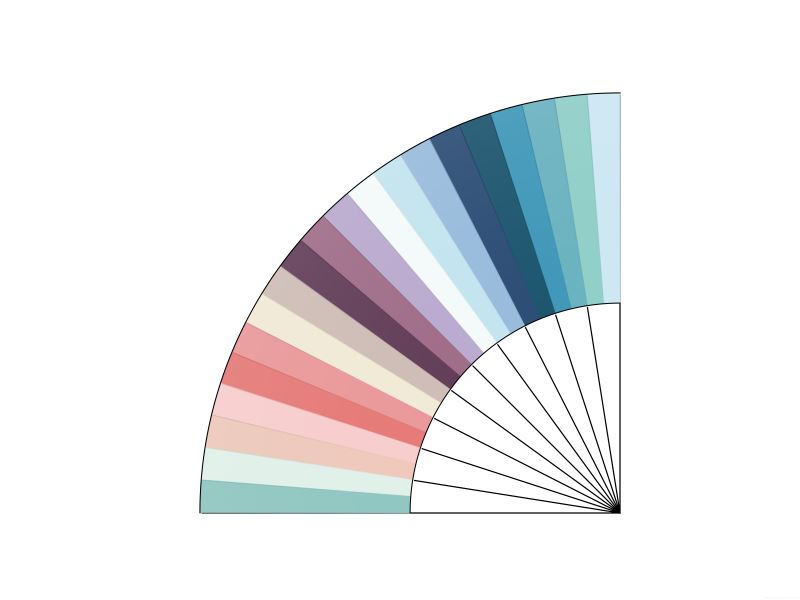
以上是我在实践过程中遇到无法使用Python库函数填充图形时采取的办法,该方法很好的诠释了数学中“点动成线,线动成面”的思想,仅提供参考,无普适价值。希望对大家的学习有所帮助,也希望大家多多支持。
以上就是【Python实现不规则图形填充的思路】的全部内容了,欢迎留言评论进行交流!